In our final installment of this three-part series on optical formulas, we are going to look into compound lenses and the optical cross.
In part 1 and part 2 of our previous optical formula blogs, we dug into some mathematical formulas that need to be learned to pass an ABO test. The truth is, understanding these formulas is an important foundation to build your optical knowledge. For those like me, who do not enjoy mathematical formulas, this blog will have no algebra - so be happy!
Let me start with the basics, this might be very useful for those new to the industry.
All prescriptions written for patients have at least one power but most have two. The first power is the sphere power and the second is the cylinder power. In simple terms, the sphere power is used to correct either Myopia or Hyperopia and will be in a plus or minus power. The cylinder power is used to correct for astigmatism of the cornea. When a lens has a sphere and a cylinder power it is called a compound lens.
When we introduce the second power or cylinder, there must be a reference system in place to show where each power is located. This is done by showing the angle or meridian of each power. In a compound lens, there are two distinct powers with the power gradually changing from one to the other between each meridian.
These meridians are numbered like the angles of a circle. The horizontal line is 0 or 180 degrees, we only use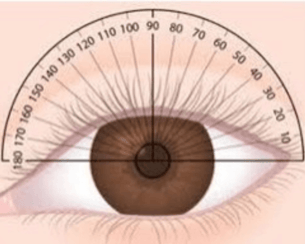
180. The vertical is 90. Meridians (axis) are oriented from the left to the right on a patient's glasses or right to left as we look at the patient (see the chart below).
So when looking at a patient, a meridian of 45 on the left will be up and toward the nasal side. The two powers, sphere and cylinder will be located exactly 90 degrees from each other.
The Optical Cross
The power of a lens and the Rx are two different things. The Rx is the representation of the power. It simply tells us where the powers are and once we diagram it out on the optical cross or power cross, we will know what the true or actual powers of a lens are.
As an example, an Rx of -1.00 -1.25 X 180 is written as a relationship between the sphere power and cylinder power. The axis is always where the sphere power is located so in this case the sphere power of -1.00 is at the axis of 180. The cylinder power is actually -1.25 more than the sphere for a total power of -2.25.
Knowing that 180° is the horizontal line and 90° is the vertical line we can map the true power of the lens using the optical cross. Along the 180° or horizontal line the power will be -1.00 and at the vertical or 90° line the power will be -2.25. The sphere power is at 180° and the total power with the cylinder will be 90° different or at the 90° meridian line.
Once this is known you will also be able to figure out the the total power in each meridian. For example: If the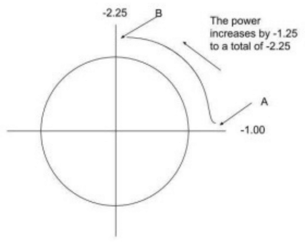
power at 180° is -1.00 and we know the power at 90 is -2.25 based upon the -1.25 cylinder, what would the power be at 45°? Because 45 is half of 90, we would simply divide the cylinder power by 2 and add that to the sphere power (1.25 ÷ 2 = .62). So the true power of a -1.00 -1.25 x 180 Rx at 45° would be -1.62.
I hope that you enjoyed learning through this series. For those new to the industry, please keep learning. How do you eat an elephant? One bite at a time. Just treat your training the same. Learn a little each day.
